Beginners’ guide#

Welcome to the absolute beginner’s guide to py-fatigue! If you have comments or suggestions, please don’t hesitate to file an issue or make a pull request on our GitHub repo: https://github.com/OWI-Lab/py_fatigue/.

Welcome to py-fatigue!#

py-fatigue was originally part of the DYNAwind suite of tools for wind turbine structural health monitoring and analysis. The tool has been detached from the project and now relies on the following PyPi packages only:

  • Python ([3.8, 3.9, 3.10], 64-bit)

  • numpy

  • plotly

  • pandas

  • numba vers. <0.57 (next year we will update to the latest version, but for now, we are stuck with this one, as it is the last one compatible with Python 3.8)

  • matplotlib

  • pydantic

The package bundles the main functionality for performing cyclic stress (fatigue and crack growth) analysis and cycle-counting.

Installing py-fatigue#

py-fatigue is freely available on GitHub and gets maintained through CI/CD phylosophy. The package requires Python 3.8 or higher, and it requires a 64-bit version of Python.

To install the toolbox, simply run:

pip install py-fatigue

and you will get the latest stable version of the toolbox.

How to import py-fatigue#

To access py-fatigue and its functions import it in your Python code like this:

import py_fatigue as pf

How to use py-fatigue#

The main functionality of py-fatigue is to perform cyclic stress analysis and cycle counting. The toolbox provides a number of functions to perform these tasks. The main functions are:

  1. cycle_count: collects all the functions related with cycle-counting fatigue data and allows a simpler representation of a rainflow-counted stress vs. time history.

  2. material: allows the definition of some fatigue-specific material properties such as

  1. geometry: enables the instantiation of specific crack geometries for crack propagation analysis, i.e.

  1. Infinite surface.

  2. Hollow cylinder with a crack on its external surface.

  1. damage: the module collecting the fatigue life calculation models.

  1. stress-life: fatigue analysis based on the cycle-counting and SN curve.

  2. crack_growth: crack propagation (growth) analysis based on the cycle-counting, the Paris’ law and the geometrical definition of a crack case (defect geometry and medium).

The toolbox also provides a number of helper functions to simulate load histories:

  • testing includes functions to simulate different kinds of load histories. The most generic type of load history can be simulated using the make_random_signal function which outputs a dw_signal.Signal object.

Example#

In the following example, starting from a randomly generated signal, we will:

  • calculate the rainflow

  • export the cycle-count matrix

  • reconstruct the CycleCount object from the exported matrix

  • define the SN curve

  • calculate the Palmgren-Miner damage

  • define the Paris’ law

  • define a crack geometry

  • run a crack growth analysis.

The damage and crack growth analyses will be also executed by means of the pandas DataFrame accessors that py-fatigue implements.

Random signal simulation#

import py_fatigue as pf
import py_fatigue.testing as test

# Simulate a random signal
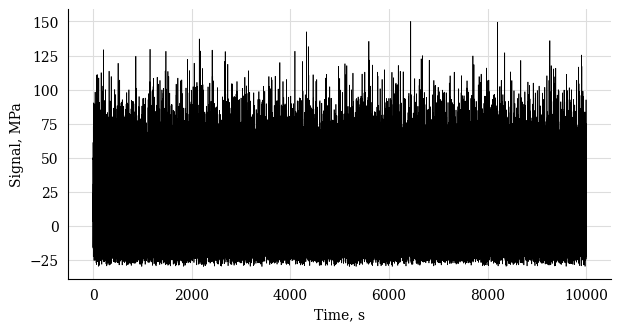
t = test.get_sampled_time(duration=10000, fs=10)
s = test.get_random_data(
    t=t, min_=-30, range_=180, random_type="weibull", a=2., seed=42
)
# Plot the signal
plt.plot(t, s, 'k', lw=0.5)
plt.xlabel("Time, s")
plt.ylabel("Signal, MPa")
plt.show()
../_images/make_random_signal_1.png

Cycle-count definition#

# CycleCount definition
cycle_count = pf.CycleCount.from_timeseries(
    time=t, data=s, mean_bin_width=3., range_bin_width=3.,
)
cycle_count

Cycle counting object

Random signal

largest full stress range, MPa

179.026964

largest stress range, MPa

180.0

number of full cycles

33317

number of residuals

23

number of small cycles

0

stress concentration factor

N/A

residuals resolved

False

mean stress-corrected

No

Cycle-count matrix#

# Exporting the cycle-count matrix in the legacy format, i.e. not
# accounting for mean stresses. This function has been kept for
# backwards compatibility.
exp_dict_legacy = cycle_count.as_dict(
    max_consecutive_zeros=20, damage_tolerance_for_binning=0.2, legacy=True
)
print(exp_dict_legacy)

{"nr_small_cycles": 99, "range_bin_lower_bound": 0.2, "range_bin_width": 3.0,
 "hist": [1346.0, 1485.0, 1433.0, 1397.0, 1455.0, 1493.0, 1479.0, 1471.0, 1348.0,
          1432.0, 1361.0, 1234.0, 1236.0, 1203.0, 1146.0, 1103.0, 1072.0,  983.0,
           957.0,  853.0,  808.0,  806.0,  679.0,  659.0,  570.0,  520.0,  449.0,
           451.0,  397.0,  376.0,  289.0,  259.0,  236.0,  237.0,  164.0,  160.0,
           120.0,   89.0,   85.0,   92.0,   60.0,   54.0,   39.0,   20.0,   24.0,
            24.0,   17.0,   12.0,   10.0,    8.0,    2.0,    5.0,    6.0,    1.0,
             0.0,    2.0,    0.0,    1.0,    0.0,    1.0], "lg_c": [],
 "res": [ 64.9527,  76.1706,  83.8523, 112.9550, 115.8100, 123.7286, 125.4990,
         137.6065, 138.7786, 139.5674, 140.8493, 159.0391, 159.1209, 167.0853,
         167.1570, 180.0000, 179.8804, 122.3010, 115.1474,  58.9131,  53.7620,
          31.8885],
 "res_sig": [ 49.8674, -15.0853,  61.0853, -22.7670,  90.1880, -25.6220,  98.1066,
             -27.3924, 110.2141, -28.5645, 111.0029, -29.8464, 129.1926, -29.9283,
             137.157,  -30.0000, 150.0000, -29.8804,  92.4207, -22.7267,  36.1864,
             -17.5756, 14.3128, 14.2784]}

# Exporting the cycle-count matrix
exp_dict = cycle_count.as_dict(
    max_consecutive_zeros=20, damage_tolerance_for_binning=1
)
print(exp_dict)

{"nr_small_cycles": 99, "range_bin_lower_bound": 0.2, "range_bin_width": 3.0,
 "mean_bin_lower_bound": -25.5, "mean_bin_width": 3.0,
 "hist": [[ 0.0,  1.0],
          [ 1.0,  1.0],
          [ 4.0,  5.0,  4.0,  1.0,  3.0],
          [14.0, 17.0,  9.0, 10.0,  6.0,  4.0,  0.0,  2.0,  1.0],
          [31.0, 31.0, 21.0, 20.0, 13.0, 10.0,  6.0,  7.0,  4.0,  5.0],
          [33.0, 51.0, 24.0, 39.0, 31.0, 28.0, 22.0, 15.0, 13.0,  6.0,  2.0,  3.0,
           1.0],
          [56.0, 68.0, 63.0, 40.0, 45.0, 40.0, 36.0, 41.0, 19.0, 22.0, 18.0, 11.0,
            7.0,  2.0,  1.0],
          [74.0, 91.0, 78.0, 60.0, 78.0, 60.0, 75.0, 46.0, 44.0, 44.0, 40.0, 20.0,
           19.0, 18.0,  4.0,  2.0],
          ...,
          [ 0.0,  2.0,  0.0,  1.0,  0.0,  0.0,  0.0,  0.0,  1.0,  0.0,  0.0,  0.0,
            1.0,  0.0,  0.0,  0.0,  1.0],
          [ 0.0,  0.0,  0.0,  0.0,  0.0,  0.0,  1.0,  0.0,  0.0,  0.0,  0.0,  0.0,
            0.0,  0.0,  0.0,  0.0,  1.0],
          [0.0,  0.0,  0.0,  0.0,  1.0]],
 "lg_c": [[ 52.7204, 157.4858], [ 52.7330, 165.3195], [ 53.0368, 165.7063],
          [ 56.1889, 172.3578], [ 59.9228, 179.0270]],
 "res": [[  17.3910,  64.9527], [ 23.0000,  76.1706], [19.1591,  83.8523],
         [  33.7105, 112.9550], [ 32.2830, 115.8100], [36.2423, 123.7286],
         [  35.3571, 125.4990], [ 41.4109, 137.6065], [40.8248, 138.7786],
         [  41.2192, 139.5674], [ 40.5782, 140.8493], [49.6731, 159.0391],
         [  49.6322, 159.1209], [ 53.6143, 167.0853], [53.5785, 167.1570],
         [  60.0000, 180.0000], [ 60.0598, 179.8804], [31.2702, 122.3010],
         [  34.8470, 115.1474], [  6.7298,  58.9131], [ 9.3054,  53.7620],
         [  -1.6314, 31.8885]],
 "res_sig": [ 49.8674, -15.0853,  61.0853, -22.7670,  90.1880, -25.6220,  98.1066,
             -27.3924, 110.2141, -28.5645, 111.0029, -29.8464, 129.1926, -29.9283,
             137.1570, -30.0000, 150.0000, -29.8804, 92.4207,  -22.7267,  36.1864,
             -17.5756, 14.3128, 14.2784]}

# Reconstructing the CycleCount instance from the exported matrix
cycle_count_d = pf.CycleCount.from_rainflow(exp_dict, name="Random Signal")
cycle_count_d

Cycle counting object

Random Signal

largest full stress range, MPa

179.027

largest stress range, MPa

180.0

number of full cycles

33219

number of residuals

22

number of small cycles

99

stress concentration factor

N/A

residuals resolved

False

mean stress-corrected

No

 
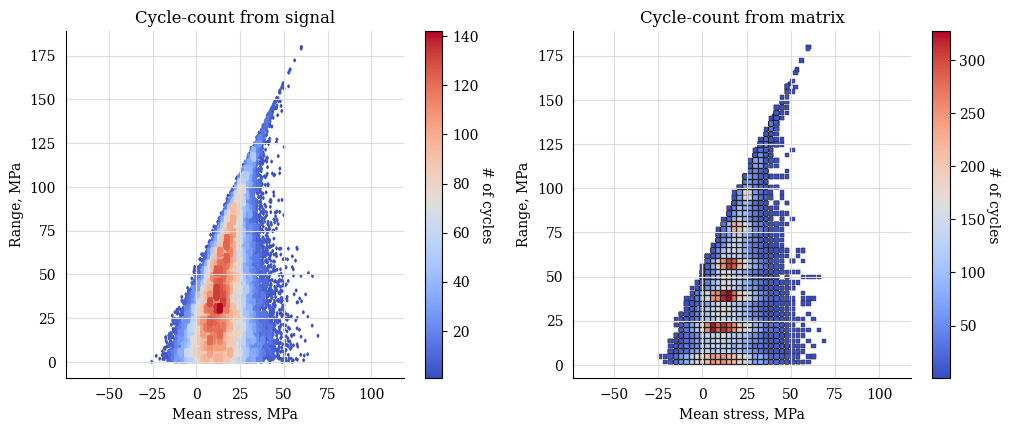
import matplotlib as mpl
import matplotlib.pyplot as plt
fig, axs = plt.subplots(1, 2, figsize=(12, 4.5))
cycle_count.plot_histogram(fig=fig, ax=axs[0], plot_type="mean-range",
                           marker="d", s=2, cmap=mpl.cm.get_cmap("coolwarm"))
axs[0].set_title("Cycle-count from signal")
cycle_count_d.plot_histogram(fig=fig, ax=axs[1], plot_type="mean-range",
                             marker="s", s=10, edgecolors="#222",
                             cmap=mpl.cm.get_cmap("coolwarm"), linewidth=0.25)
axs[1].set_title("Cycle-count from matrix")
plt.show()
../_images/cc_plot_histogram.png

Stress-Life#

SN Curve definition#

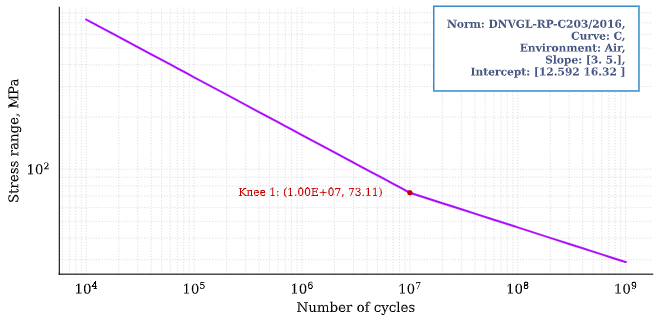
c_air = pf.SNCurve(
    [3, 5],
    intercept=[12.592, 16.320],
    norm="DNVGL-RP-C203/2016",
    environment='Air',
    curve='C'
)
c_air
../_images/sn_curve_1.png

Damage calculation analysis#

# Calculate damage for the cycle-count objects
damage = pf.damage.get_pm(cycle_count=cycle_count, sn_curve=c_air)
damage_d = pf.damage.get_pm(cycle_count=cycle_count_d, sn_curve=c_air)
print(f"damage from signal: {sum(damage)}")
print(f"damage from matrix: {sum(damage_d)}")

damage from signal: 0.0013318803351252439
damage from matrix: 0.0013321255571107358

Crack growth#

A crack growth simulation necessitates of three ingredients (objects):

  • Cycle-counted stress history

  • Crack growth curve (e.g. Paris’ law)

  • Crack geometry

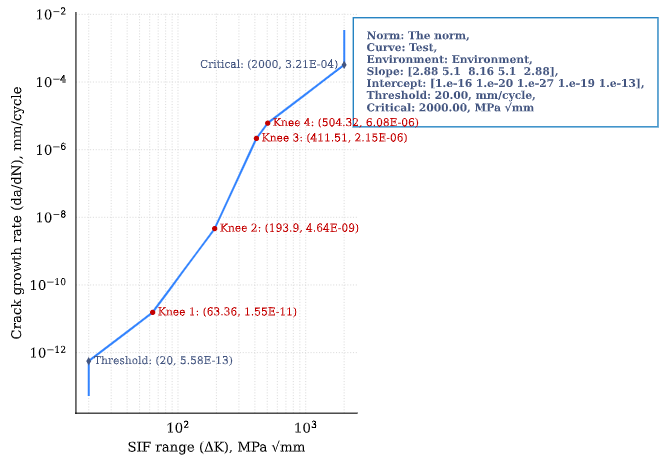
Paris’ curve definition#

SIF = np.linspace(1,2500, 300)
SLOPE = np.array([2.88, 5.1, 8.16, 5.1, 2.88])
INTER = np.array([1E-16, 1E-20, 1E-27, 1E-19, 1E-13])
THRESHOLD = 20
CRITICAL = 2000
pc = pf.ParisCurve(slope=SLOPE, intercept=INTER, threshold=THRESHOLD,
                   critical=CRITICAL, norm="The norm",
                   environment="Environment", curve="nr.")
pc
../_images/cg_curve_1.png

Crack geometry definition#

geo = pf.geometry.HollowCylinder(
  initial_depth=5.,
  thickness=10.,
  height=30.,
  outer_diameter=30.,
  crack_position="external"
)
geo

HollowCylinder(
  _id=HOL_CYL_01,
  initial_depth=5.0,
  outer_diameter=300.0,
  thickness=10.0,
  height=30.0,
  crack_position=external,
)

Crack growth analysis#

cg = pf.crack_growth.get_crack_growth(
  cycle_count, pc, geo, express_mode=True
)
print(f"Cycles to end: {int(cg.final_cycles)}")

Fatigue spectrum applied w/o failure. Stopping calculation
Cycles to end: 3328

cg_d = pf.crack_growth.get_crack_growth(
  cycle_count_d, pc, geo, express_mode=True
)
print(f"Cycles to end: {int(cg.final_cycles)}")

Fatigue spectrum applied w/o failure. Stopping calculation
Cycles to end: 3320

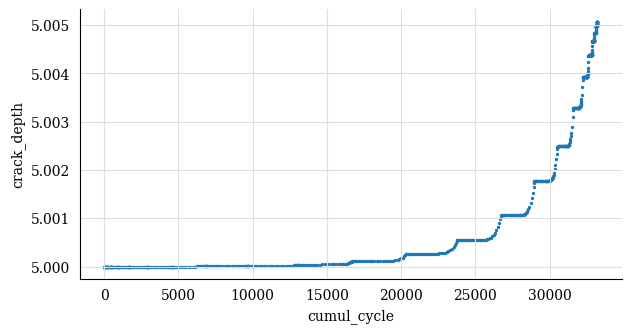
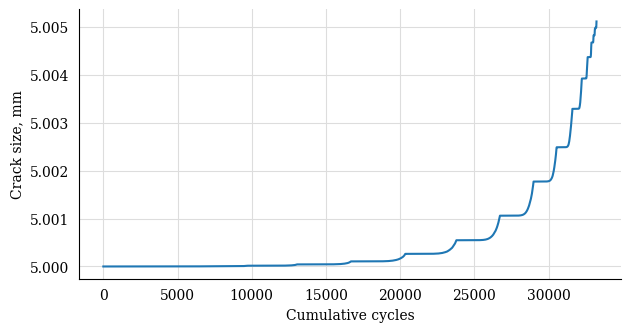
plt.plot(np.cumsum(cg_d.count_cycle), cg_d.crack_depth)
plt.xlabel("Cumulative cycles")
plt.ylabel("Crack size, mm")
plt.show()
../_images/cg_analysis_1.png

Working with pandas DataFrames#

It’s possible to translate the CycleCount object to a pandas DataFrame and use the implemented accessors py_fatigue.damage.stress_life.PalmgrenMiner (miner) and py_fatigue.damage.crack_growth.CrackGrowth (cg) to perform the stress-life and propagation analyses as shown above.

import pandas as pd

df = cycle_count.to_df()

# Stress-life
df.miner.damage(sn_curve=c_air)
# Crack-growth
df.cg.calc_growth(cg_curve=pc, crack_geometry=geo)

df.miner.plot_histogram()
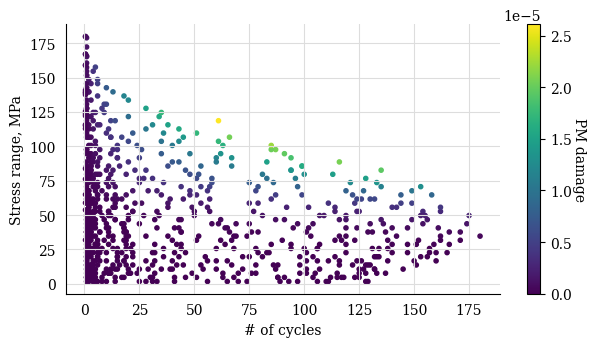
../_images/cc_plot_histogram_df.png 
df.plot(kind="scatter", x="cumul_cycle", y="crack_depth", s=2)
../_images/cg_analysis_1_df.png