7. Stress-Life damage calculation#

This section contains some examples of damage calculations using the stress-life approach.

The module py_fatigue.damage.stress_life contains all the damage models related to the stress-life approach.

The simplest and most common damage model is the Palmgren-Miner (py_fatigue.damage.stress_life.calc_pm, py_fatigue.damage.stress_life.get_pm) model.

\[D = \sum_{j=1}^{N_{\text{blocks}}} \frac{n_j}{N_j} \leq 1\]

Besides the linear damage accumulation rule, py-fatigue also provides a series of nonlinear damage accumulation models callable through py_fatigue.damage.stress_life.calc_nonlinear_damage and py_fatigue.damage.stress_life.get_nonlinear_damage

  • Manson and Halford

  • Si Jian et al.

  • Pavlou

  • Leve

The generic form of a nonlinear damage rule is:

\[D = \left( \left( \dots \left( \left( \left(\frac{n_1}{N_1}\right)^{e_{1, 2}} + \frac{n_2}{N_2} \right)^{e_{2, 3}} + \frac{n_3}{N_3} \right)^{e_{3, 4}} + \dots + \frac{n_{M-1}}{N_{M-1}} \right)^{e_{M-1, M}} + \dots + \frac{n_M}{N_M} \right)^{e_M}\]

where \(n_j\) is the number of cycles in the fatigue histogram at the \(j\)-th cycle, \(N_j\) is the number of cycles to failure at the \(j\)-th cycle, \(e_{j, j+1}\) is the exponent for the \(j\)-th and \(j+1\)-th cycles, \(M\) is the number of load blocks in the fatigue spectrum.

The formula is conveniently rewritten as pseudocode:

pseudocode for the nonlinear damage rule#
# retrieve N_j using the fatigue histogram and SN curve
# retrieve the exponents e_{j, j+1}
#  calculate the damage
D = 0
for j in range(1, M+1):
    D = (D + n_j / N_j) ^ e_{j, j+1}

Specifically, for the damage models currently implemented in py_fatigue, the exponents are:

  • Manson and Halford: \(e_{j, j+1} = \left(\frac{N_{j}}{N_{j+1}}\right)^{\alpha}\) with \(\alpha=0.4\) usually.

  • Si Jian et al.: \(e_{j, j+1} = \sigma_{j+1} / \sigma_{j}\) where \(\sigma_{j+1}\) is the stress amplitude for the \(j\)-th cycle.

  • Pavlou: \(e_{j, j+1} = \left(\frac{\Delta \sigma_j / 2}{\sigma_U}\right)^{\alpha}\) where \(\Delta \sigma_j/2\) is the stress amplitude, \(\sigma_U\) is the ultimate stress, \(\Delta \sigma\) is the stress range and \(\alpha=0.75\) (usually) is the exponent.

  • Leve: \(e_{j, j+1} =\text{constant}\).

1. Palmgren-Miner#

a. Constant fatigue load (sinoid)#

Note

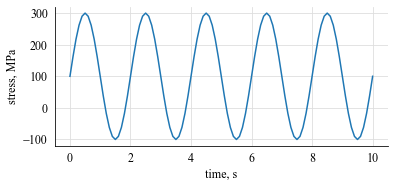
In this example we define a fatigue stress signal in the form of a sinusoidal function and calculate the damage using the Palmgren-Miner Rule.

We then feed our signal to the CycleCount class.

Define the time and stress arrays

t = np.arange(0, 10.1, 0.1)  # (in seconds)
s = 200 * np.sin(np.pi*t) + 100   # (in MPa)
plt.plot(t, s)
plt.xlabel("time, s")
plt.ylabel("stress, MPa")
plt.show()
../../_images/sine_wave.png

Define the CycleCount instance

cc = pf.CycleCount.from_timeseries(s, t, name="Example")
cc
CycleCount from constant time series#

Example

Cycle counting object

largest full stress range, MPa,

None

largest stress range, MPa

400.0

number of full cycles

0

number of residuals

11

number of small cycles

0

stress concentration factor

N/A

residuals resolved

False

mean stress-corrected

No

Define the SN curve

1w3a = pf.SNCurve([3, 5], [10.970, 13.617],
2                 norm='DNVGL-RP-C203', curve='W3', environment='Air')

There are two main ways of calculating the damage from cc.

  1. Using the get_pm() method.

  2. Converting cc to a DataFrame and using the dataframe extension called df.miner.damage().

1df = cc.to_df()
2df.miner.damage(w3a)
3print(df)
4print(f"Damage from pandas df: {df['pm_damage'].sum()}")
5print(f"Damage from  function: {pf.stress_life.get_pm(cc, w3a)}")

Which outputs:

index

count_cycle

mean_stress

stress_range

cycles_to_failure

pm_damage

0

0.5

200

200

11665.68

0.000043

1

0.5

100

400

1458.21

0.000343

2

0.5

100

400

1458.21

0.000343

3

0.5

100

400

1458.21

0.000343

4

0.5

100

400

1458.21

0.000343

5

0.5

100

400

1458.21

0.000343

6

0.5

100

400

1458.21

0.000343

7

0.5

100

400

1458.21

0.000343

8

0.5

100

400

1458.21

0.000343

9

0.5

100

400

1458.21

0.000343

10

0.5

0

200

11665.68

0.000043

 
Damage from pandas df: 0.0031716971435032985
Damage from  function: 0.0031716971435032985